Perlin noise

Perlin noise is a computer-generated visual effect developed by Ken Perlin, who won an Academy Award for its use in the motion picture Tron. It can be used to simulate elements from nature, and is especially useful in circumstances where computer memory is limited.

Contents

Uses

Perlin noise is a procedural texture primitive, a type of gradient noise used by visual effects artists to increase the appearance of realism in computer graphics. The function has a pseudo-random appearance, yet all of its visual details are the same size (see image). This property allows it to be readily controllable; multiple scaled copies of Perlin noise can be inserted into mathematical expressions to create a great variety of procedural textures. Synthetic textures using Perlin noise are often used in CGI to make computer-generated visual elements - such as fire, smoke, or clouds - appear more natural, by imitating the controlled random appearance of textures of nature.

It is also frequently used to generate textures when memory is extremely limited, such as in demos, and is increasingly finding use in Graphics Processing Units for real-time graphics in computer games.

Development

Perlin noise resulted from the work of Ken Perlin, who developed it while working at Mathematical Applications Group, Inc.. In 1997, he won an Academy Award for Technical Achievement from the Academy of Motion Picture Arts and Sciences for this contribution to the 1982 film Tron.[1]

Algorithm

Perlin noise is most commonly implemented as a function of either (x,y), (x,y,z) or (x,y,z,w), but can be defined for any number of dimensions.

Define an n-dimensional grid. Each grid coordinate stores a gradient of unit length in n dimensions. To sample, determine which grid cell you're in, and then compute the n-dimensional vectors from the sample location to each grid coordinate of the cell. For each of grid coordinate, calculate the dot products of the corresponding distance and gradient vectors. Finally, interpolate these dot products using a function that has first derivative = 0 at both endpoints, (and possibly second derivative too).

In 2002, Ken Perlin created Simplex noise, which is similar to but alleviates some problems with Perlin "Classic Noise", among them, computational complexity.

Complexity

For n being the number of dimensions, Perlin Noise has complexity 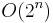O(2^n) while Simplex Noise has complexity O(n).

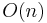See also

References

  1. ^ Kerman, Phillip. Macromedia Flash 8 @work: Projects and Techniques to Get the Job Done. Sams Publishing. 2006.

External links